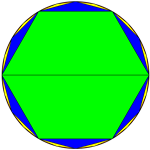
割圆术 (刘徽)
近期热点
资料介绍
圆周率:
3.1415926535897932384626433...
运用:
圆的面积周长含圆周率的公式列表
证明:
无理性超越性
值:
约率(证明22/7大于π)密率近似值割圆术
人物:
阿基米德刘徽祖冲之玛达瓦(英语:Madhava of Sangamagrama)威廉·琼斯约翰·梅钦约翰·伦奇鲁道夫·范科伊伦阿耶波多
历史:
年表
文化:
节日
相关主题:
化圆为方巴塞尔问题连续的六个9
查论编
割圆术是中国古代数学中“一个十分精彩的算法”。在此之前,圆周率采用“径一周三”的实验数据。东汉科学家张衡采用和。刘徽认为过大。。东汉天文学家王蕃采用。这些圆周率都是实验值,都只准确到二位数字。刘徽是中国数学史上最先创造了一个从数学上计算圆周率到任意精确度的迭代程序的数学家。他自己通过分割圆为192边形,计算出圆周率在3.141024 与 3.142704之间,取其近似,并以 表示。这个数值准确到三位数字,比前人的圆周率数值都准,但他自己次承认这个数值偏小。后来刘徽发明一种快捷算法,可以只用96边形得到和1536边形同等的精确度,从而得令他自己满意的。
刘徽割圆术简单而又严谨,富于程序性,可以继续分割下去,求得更精确的圆周率。南北朝时期著名数学家祖冲之用刘徽割圆术计算11次,分割圆为12288边形,得圆周率=3.1415926,成为此后千年世界上最准确的圆周率。
标签: 数学家
相关热点
最新收录
- 彩乃圣罗(彩乃せいら) 07-24
- 心阳希美(心陽のぞ美) 07-24
- 七绪绯美佳(七緒ひみか 07-24
- 阳野爱实(陽野めぐみ) 07-24
- 1818黄金眼郑女士 07-24
- 发际线男孩小吴 07-24
- 乔瓦尼·多梅尼科·马拉迪 07-24
- 夏尔-欧仁·德洛奈 07-23
- 板垣公一 07-23
- 平山清次 07-23