割圆术 (赵友钦)
近期热点
资料介绍
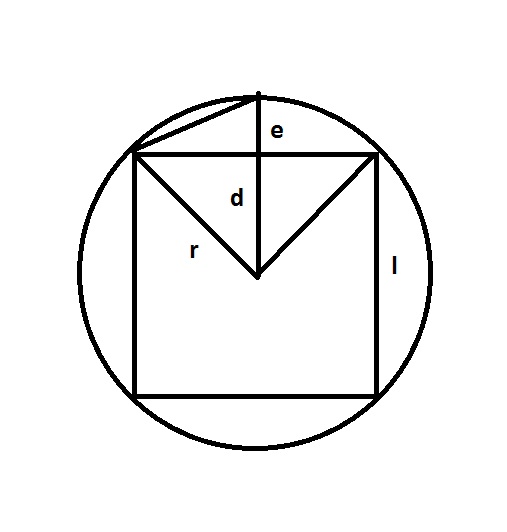
赵友钦割圆术是元代数学家赵友钦在所著的《革象新书卷五《乾象周髀篇研究的割圆术。与刘徽从内接正六角形开始不同,赵氏割圆术从分割内接正方形开始。
如图,圆的半径为r; 内接正方形的边长为 ,由圆心到正方形一边倒垂直距离为 d
d 的延长线与圆周相交点将圆周等分为正八边形。
令正八边形的边长为
设 为分割圆成正16边形之边长,赵友钦正确地推断与的迭代关系:
推而广之:
令 r=1;
……
标签: 数学家
相关热点
最新收录
- 彩乃圣罗(彩乃せいら) 07-24
- 心阳希美(心陽のぞ美) 07-24
- 七绪绯美佳(七緒ひみか 07-24
- 阳野爱实(陽野めぐみ) 07-24
- 1818黄金眼郑女士 07-24
- 发际线男孩小吴 07-24
- 乔瓦尼·多梅尼科·马拉迪 07-24
- 夏尔-欧仁·德洛奈 07-23
- 板垣公一 07-23
- 平山清次 07-23